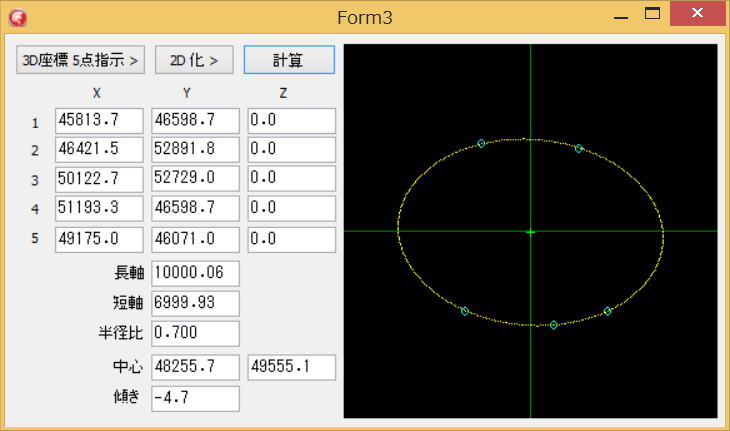
■ 3D平面上の 5 点を通る楕円
CAD上で、3D 座標 5 点を指示します。
この 5 点のうち代表 3 点を通る平面を、X-Y平面に合わせるため、Z軸、Y軸、X軸を回転します。
結果、5 点の Z 値は、0 になります。
楕円の方程式 : AX^2 + BXY + CY^2 + DX + EY + 1 = 0 に、5 点の X,Y を代入すると、5 元連立方程式が出来ます。
これを、ガウス-ジョルダン法で解くと、変数 A, B, C, D, E が求まります。
(参考URL:「オッズ シェアの計算方法 - TigerOddsの最終レース日記」 http://ameblo.jp/tigerodds/entry-10060455494.html)
これらから、近似楕円の長軸、短軸、中心を求めます。
(参考URL:「最小二乗法による楕円近似 - 画像処理ソリューション」 http://imagingsolution.blog107.fc2.com/blog-entry-20.html)
※座標の取得、検証に Bricscad を使っていますが、計算には不要です。
■ ソースコード
unit Gauss2Unit;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls,BricscadApp_TLB,BricscadDB_TLB, ComObj, Math,
Vcl.ExtCtrls;
type
TForm3 = class(TForm)
Button2: TButton;
Edit6: TEdit;
Edit7: TEdit;
Edit8: TEdit;
Edit9: TEdit;
Edit10: TEdit;
Edit11: TEdit;
Edit12: TEdit;
Edit13: TEdit;
Edit14: TEdit;
Edit15: TEdit;
Edit22: TEdit;
Edit23: TEdit;
Edit26: TEdit;
Label7: TLabel;
Label8: TLabel;
Label9: TLabel;
Label10: TLabel;
Label11: TLabel;
Label12: TLabel;
Label13: TLabel;
Label16: TLabel;
Label17: TLabel;
Label18: TLabel;
Image1: TImage;
Edit21: TEdit;
Edit24: TEdit;
Label1: TLabel;
Edit25: TEdit;
Label2: TLabel;
Button4: TButton;
Button5: TButton;
Label5: TLabel;
Edit35: TEdit;
Edit36: TEdit;
Edit37: TEdit;
Edit38: TEdit;
Edit39: TEdit;
procedure Button2Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure Button4Click(Sender: TObject);
procedure Button5Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
type
TGaussA = array[0..17, 0..17] of Extended;
type
TGaussB = array[0..17] of Extended;
type
cadpt = array[0..2] of double;
var
Form3: TForm3;
cadpts : array of cadpt;
implementation
{$R *.dfm}
//Z軸まわりに座標を回転
function Rotate(pt:cadPt;rad:extended):cadPt;
var
cosz,sinz:extended;
begin
cosz := Cos(rad);
sinz := Sin(rad);
Result[0] := pt[0] * cosz + pt[1] * -sinz;
Result[1] := pt[0] * sinz + pt[1] * cosz;
Result[2] := pt[2];
end;
function RotateBase(base, pt: cadPt; rad: extended): cadPt;
var
cosz,sinz:extended;
begin
cosz := Cos(rad);
sinz := Sin(rad);
Result[0] := base[0] + (pt[0] - base[0]) * cosz + (pt[1] - base[1]) * -sinz;
Result[1] := base[1] + (pt[0] - base[0]) * sinz + (pt[1] - base[1]) * cosz;
Result[2] := pt[2];
end;
//Y軸まわりに座標を回転
function RotateYAx(pt: cadPt; rad: extended): cadPt;
var
cosy,siny:extended;
begin
cosy := Cos(rad);
siny := Sin(rad);
Result[0] := pt[0] * cosy + pt[2] * siny;
Result[1] := pt[1];
Result[2] := pt[0] * -siny + pt[2] * cosy;
end;
//X軸まわりに座標を回転
function RotateXAx(pt:cadPt;rad:extended):cadPt;
var
cosx,sinx:extended;
begin
cosx := Cos(rad);
sinx := Sin(rad);
Result[0] := pt[0];
Result[1] := pt[1] * cosx + pt[2] * -sinx;
Result[2] := pt[1] * sinx + pt[2] * cosx;
end;
//****************************************
// 2d距離
//****************************************
function Distance(p1, p2: cadPt):extended;
begin
Result := sqrt(sqr(p1[1] - p2[1]) + sqr(p1[0] - p2[0]));
end;
//****************************************
// 線分2点の角度
//****************************************
function Angle(p1, p2: cadPt): extended;
var
ang, x, y : extended;
begin
x := p2[0] - p1[0];
y := p2[1] - p1[1];
if abs(x) < 10e-6 then begin
if p1[1] < p2[1] then ang := pi * 0.5 else ang := pi * 1.5;
end
else if abs(y)< 10e-6 then begin
if p1[0] < p2[0] then ang := 0 else ang := pi;
end
else begin
ang := abs(ArcTan(y / x));
if (x < 0.0) and (y >= 0.0) then ang := pi - ang
else if (x >= 0.0) and (y < 0.0) then ang := pi * 2.0 - ang
else if (x < 0.0) and (y < 0.0) then ang := ang + pi;
end;
result := ang;
end;
//****************************************
// 座標:p0から角度:radの距離:distの点を求める
//****************************************
function Polar(p0: cadPt; rad, dist: double): cadPt;
begin
result[0] := dist * cos(rad) + p0[0];
result[1] := dist * sin(rad) + p0[1];
result[2] := p0[2];
end;
//****************************************
// 連立方程式ガウス-ジョルダン法 Delphi
// n:n次方程式 a:係数を表すn次元配列
// b:非同次項を表す1次配列
// 戻り値:a:逆行列 b:解
// type TGaussA=array[0..17,0..17] of real; //添え字の上限=n-1
// type TGaussB=array[0..17] of real; //添え字の上限=n-1
//
// 引用元:「オッズ シェアの計算方法 - TigerOddsの最終レース日記」
// http://ameblo.jp/tigerodds/entry-10060455494.html
// その元
// http://akita-nct.jp/yamamoto/lecture/2004/5E/linear_equations/how_to_make_GJ/gaussj.pdf
//****************************************
function gauss_jordan(n: integer; var a: TGaussA; var b: TGaussB): boolean;
var
ipv, i, j : integer;
inv_pivot, temp : real;
big : real;
pivot_row : integer;
row : array[0..17] of integer;
begin
result := True;
pivot_row := -1;
for ipv := 0 to n - 1 do begin
//最大値検索
big := 0.0;
for i := ipv to n - 1 do begin
if abs(a[i, ipv]) > big then begin
big := abs(a[i, ipv]);
pivot_row := i;
end;
end;
if big = 0 then begin
Result := False;
Exit;
end;
row[ipv] := pivot_row;
// 行の入れ替え
if (ipv <> pivot_row) then begin
for i := 0 to n - 1 do begin
temp := a[ipv, i];
a[ipv, i] := a[pivot_row, i];
a[pivot_row, i] := temp;
end;
temp := b[ipv];
b[ipv] := b[pivot_row];
b[pivot_row] := temp;
end;
// 対角成分=1 ピボット行の処理
inv_pivot := 1.0 / a[ipv, ipv];
a[ipv,ipv] := 1.0;
for j := 0 to n - 1 do begin
a[ipv, j] := a[ipv, j] * inv_pivot;
end;
b[ipv] := b[ipv] * inv_pivot;
// ピボット列=0 ピボット行以外ノ処理
for i := 0 to n - 1 do begin
if (i <> ipv) then begin
temp := a[i, ipv];
a[i, ipv] := 0.0;
for j := 0 to n - 1 do begin
a[i, j] := a[i,j] - temp * a[ipv, j];
end;
b[i] := b[i] - temp * b[ipv];
end;
end;
end;
// 列の入れ替え(逆行列)
for j := n - 1 downto 0 do begin
if (j <> row[j]) then begin
for i := 0 to n - 1do begin
temp := a[i, j];
a[i, j] := a[i, row[j]];
a[i, row[j]] := temp;
end;
end;
end;
end;
// 変数計算
procedure TForm3.Button2Click(Sender: TObject);
var
i : integer;
Ga: TGaussA; Gb: TGaussB;
A, B, C, D, E : Extended;
xx,yy:array [0..4] of double;
sc : double;
x0, y0, ang : double;
ra, rb, temp : double;
p0, p1 :cadpt;
begin
Edit22.Text := '---';
Edit23.Text := '---';
Edit26.Text := '---';
with Image1 do begin
Canvas.Brush.Color := clBlack;
Canvas.FillRect(Rect(0,0,Width,Height));
end;
xx[0] := StrToFloat(Edit6.Text);
yy[0] := StrToFloat(Edit7.Text);
xx[1] := StrToFloat(Edit8.Text);
yy[1] := StrToFloat(Edit9.Text);
xx[2] := StrToFloat(Edit10.Text);
yy[2] := StrToFloat(Edit11.Text);
xx[3] := StrToFloat(Edit12.Text);
yy[3] := StrToFloat(Edit13.Text);
xx[4] := StrToFloat(Edit14.Text);
yy[4] := StrToFloat(Edit15.Text);
// 楕円の方程式:AX^2 + BXY + CY^2 + DX + EY + 1 = 0
for i := 0 to 4 do begin
Ga[i, 0] := xx[i] * xx[i];
Ga[i, 1] := xx[i] * yy[i];
Ga[i, 2] := yy[i] * yy[i];
Ga[i, 3] := xx[i];
Ga[i, 4] := yy[i];
Gb[i] := -1;
end;
// 連立方程式をガウス-ジョルダン法で解く
if gauss_jordan(5, Ga, Gb) then begin
// 「最小二乗法による楕円近似 - 画像処理ソリューション」
// http://imagingsolution.blog107.fc2.com/blog-entry-20.html
//
// aX^2 + bXY + cY^2 + dX + eY + 1 = 0 を
// X^2 + AXY + BY^2 + CX + DY + E = 0 の形にするため、
// すべての変数を a で割る
A := Gb[1] / Gb[0];
B := Gb[2] / Gb[0];
C := Gb[3] / Gb[0];
D := Gb[4] / Gb[0];
E := 1 / Gb[0];
// 中心の座標
x0 := (A * D - 2 * B * C) / (4 * B - A * A);
y0 := (A * C - 2 * D) / (4 * B - A * A);
// 傾き
ang := ArcTan(A /(1 - B)) / 2.0;
// X座標
Edit21.Text := Format('%.1f', [x0]);
// Y座標
Edit24.Text := Format('%.1f', [y0]);
// 傾き
Edit25.Text := Format('%.1f', [RadToDeg(ang)]);
// X軸方向の長さA
ra := sqrt(sqr(x0 * cos(ang) + y0 * sin(ang)) - E * sqr(cos(ang)) -
(sqr(x0 * sin(ang) - y0 * cos(ang)) - E * sqr(sin(ang))) *
(sqr(sin(ang)) - B * sqr(cos(ang))) / (sqr(cos(ang))- B * sqr(sin(ang))));
// Y軸方向の長さB
rb := sqrt(sqr(x0 * sin(ang) - y0 * cos(ang)) - E * sqr(sin(ang)) -
(sqr(x0 * cos(ang) + y0 * sin(ang)) - E * sqr(cos(ang))) *
(sqr(cos(ang)) - B * sqr(sin(ang))) / (sqr(sin(ang)) - B * sqr(cos(ang))));
if ra > rb then begin
// 長軸
Edit22.Text := Format('%.2f', [ra * 2]);
// 短軸
Edit23.Text := Format('%.2f', [rb * 2]);
// 短軸/長軸の比
Edit26.Text := Format('%.3f', [rb / ra]);
{
// 切断角度
if (ra > 0) and ((rb/ra) <= 1) then
Edit27.Text := Format('%.2f', [RadToDeg(pi / 2 - arccos(rb/ra))])
else
Edit27.Text := '---';
}
end
else begin
// 長軸
Edit22.Text := Format('%.2f', [rb * 2]);
// 短軸
Edit23.Text := Format('%.2f', [ra * 2]);
// 短軸/長軸の比
Edit26.Text := Format('%.3f', [ra / rb]);
{
// 切断角度
if (rb > 0) and ((ra / rb) <= 1) then
Edit27.Text := Format('%.2f', [RadToDeg(pi / 2 - arccos(ra/rb))])
else
Edit27.Text := '---';
}
end;
p0[0] := x0;
p0[1] := y0;
with Image1 do begin
if ra > rb then
sc := ra * 2 * 1.4 / width
else
sc := rb * 2 * 1.4 / width;
// 指示された5点を描画
Canvas.Pen.Color := clAqua;
for i := 0 to 4 do begin
Canvas.Ellipse(
Trunc((xx[i] - x0) / sc) + width div 2 + 3,
Height - Trunc((yy[i] - y0) / sc) - width div 2 + 4,
Trunc((xx[i] - x0) / sc) + width div 2 - 3,
Height - Trunc((yy[i] - y0)/ sc) - width div 2 - 3);
end;
// 中心点「+」マーク
Canvas.Pen.Color := clGreen;
Canvas.MoveTo(0, Height div 2);
Canvas.LineTo(width, Height div 2);
Canvas.MoveTo(Width div 2, 0);
Canvas.LineTo(width div 2, Height);
Canvas.Pen.Color := clLime;
Canvas.MoveTo(Trunc((p0[0] - x0) / sc) + width div 2 - 3,
Height - Trunc((p0[1] - y0) / sc) - width div 2);
Canvas.LineTo(Trunc((p0[0] - x0) / sc) + width div 2 + 4,
Height - Trunc((p0[1] - y0) / sc) - width div 2);
Canvas.MoveTo(Trunc((p0[0] - x0)/ sc) + width div 2,
Height - Trunc((p0[1] - y0) / sc) - width div 2 - 3);
Canvas.LineTo(Trunc((p0[0] - x0) / sc) + width div 2,
Height - Trunc((p0[1] - y0) / sc) - width div 2 + 4);
// 楕円を描く
for i := 0 to 359 do begin
p1 := Polar(p0, DegToRad(i), rb);
p1[0] := p0[0] + (p1[0] - p0[0]) * (ra / rb);
p1 := RotateBase(p0, p1, ang);
Canvas.Pixels[Trunc((p1[0] - x0) / sc) + width div 2,
Height - Trunc((p1[1] - y0) / sc) - width div 2] := clYellow;
end;
end;
end;
end;
// 3D 座標 5 点指示
procedure TForm3.Button4Click(Sender: TObject);
var
app: IAcadApplication;
vpt : OleVariant;
i : integer;
xx, yy, zz : array [0..4] of double;
begin
Edit21.Text := '';
Edit22.Text := '';
Edit23.Text := '';
Edit24.Text := '';
Edit25.Text := '';
Edit26.Text := '';
with Image1 do begin
Canvas.Brush.Color := clBlack;
Canvas.FillRect(Rect(0,0,Width,Height));
end;
app := GetActiveOleObject('BricscadApp.AcadApplication') as IAcadApplication;
try
vpt := VarArrayCreate([0, 2], varDouble);
for i := 0 to 4 do begin
SetForegroundWindow(app.HWND);
vpt := app.ActiveDocument.Utility.GetPoint(EmptyParam, IntToStr(i + 1) + ' 点目を指示');
xx[i] := Trunc(vpt[0]*10) / 10;
yy[i] := Trunc(vpt[1]*10) / 10;
zz[i] := Trunc(vpt[2]*10) / 10;
end;
Edit6.Text := FloatToStr(xx[0]);
Edit7.Text := FloatToStr(yy[0]);
Edit8.Text := FloatToStr(xx[1]);
Edit9.Text := FloatToStr(yy[1]);
Edit10.Text := FloatToStr(xx[2]);
Edit11.Text := FloatToStr(yy[2]);
Edit12.Text := FloatToStr(xx[3]);
Edit13.Text := FloatToStr(yy[3]);
Edit14.Text := FloatToStr(xx[4]);
Edit15.Text := FloatToStr(yy[4]);
Edit35.Text := FloatToStr(zz[0]);
Edit36.Text := FloatToStr(zz[1]);
Edit37.Text := FloatToStr(zz[2]);
Edit38.Text := FloatToStr(zz[3]);
Edit39.Text := FloatToStr(zz[4]);
except
;
end;
end;
// 2D化(代表3点の平面を、X-Y平面に合わせる)
procedure TForm3.Button5Click(Sender: TObject);
var
pts : array[0..4] of cadpt;
dist, xang , yang, zang: double;
i, j : integer;
pt0, pt1, pt2 : cadpt;
distmax : double;
pt0x, pt0y : double;
begin
pts[0][0]:= StrToFloat(Edit6.Text);
pts[0][1]:= StrToFloat(Edit7.Text);
pts[0][2]:= StrToFloat(Edit35.Text);
pts[1][0]:= StrToFloat(Edit8.Text);
pts[1][1]:= StrToFloat(Edit9.Text);
pts[1][2]:= StrToFloat(Edit36.Text);
pts[2][0]:= StrToFloat(Edit10.Text);
pts[2][1]:= StrToFloat(Edit11.Text);
pts[2][2]:= StrToFloat(Edit37.Text);
pts[3][0]:= StrToFloat(Edit12.Text);
pts[3][1]:= StrToFloat(Edit13.Text);
pts[3][2]:= StrToFloat(Edit38.Text);
pts[4][0]:= StrToFloat(Edit14.Text);
pts[4][1]:= StrToFloat(Edit15.Text);
pts[4][2]:= StrToFloat(Edit39.Text);
// XY平面で相互距離の一番長い2点を得る
// 仮想直線とする
distmax := 0;
for i := 0 to 3 do begin
for j := i + 1 to 4 do begin
dist := Distance(pts[i], pts[j]);
if distmax < dist then begin
distmax := dist;
pt0 := pts[i];
pt1 := pts[j];
end;
end;
end;
// 元の位置
pt0x := pt0[0];
pt0y := pt0[1];
// pt0 を原点にする
// 原点に移動
for i := 0 to 4 do begin
for j := 0 to 2 do
pts[i][j] := pts[i][j] - pt0[j];
end;
for j := 0 to 2 do begin
pt1[j] := pt1[j] - pt0[j];
pt0[j] := pt0[j] - pt0[j];
end;
// 仮想直線をX軸に合わせる
zang := Angle(pt0, pt1);
// Z軸周りに回転
pt1 := Rotate(pt1, -zang);
for i := 0 to 4 do
pts[i] := Rotate(pts[i], -zang);
// y軸周りに回転
yang := ArcTan(pt1[2] / pt1[0]);
pt1 := RotateYAx(pt1, yang);
for i := 0 to 4 do
pts[i] := RotateYAx(pts[i], yang);
// y座標の一番遠い座標を得る
distmax := 0;
for i := 0 to 4 do begin
dist := abs(pts[i][1]);
if distmax < dist then begin
distmax := dist;
pt2 := pts[i];
end;
end;
// X軸周りに回転
xang := ArcTan(pt2[2] / pt2[1]);
pt2 := RotateXAx(pt2, xang);
for i := 0 to 4 do
pts[i] := RotateXAx(pts[i], -xang);
// Z軸周りの回転を戻す
for i := 0 to 4 do
pts[i] := Rotate(pts[i], zang);
// X,Yのみ元の座標に戻す
for i := 0 to 4 do begin
pts[i][0] := pts[i][0] + pt0x;
pts[i][1] := pts[i][1] + pt0y;
end;
Edit6.Text := Format('%.1f',[pts[0][0]]);
Edit7.Text := Format('%.1f',[pts[0][1]]);
Edit8.Text := Format('%.1f',[pts[1][0]]);
Edit9.Text := Format('%.1f',[pts[1][1]]);
Edit10.Text := Format('%.1f',[pts[2][0]]);
Edit11.Text := Format('%.1f',[pts[2][1]]);
Edit12.Text := Format('%.1f',[pts[3][0]]);
Edit13.Text := Format('%.1f',[pts[3][1]]);
Edit14.Text := Format('%.1f',[pts[4][0]]);
Edit15.Text := Format('%.1f',[pts[4][1]]);
Edit35.Text := Format('%.1f',[pts[0][2]]);
Edit36.Text := Format('%.1f',[pts[1][2]]);
Edit37.Text := Format('%.1f',[pts[2][2]]);
Edit38.Text := Format('%.1f',[pts[3][2]]);
Edit39.Text := Format('%.1f',[pts[4][2]]);
end;
procedure TForm3.FormCreate(Sender: TObject);
begin
with Image1 do begin
Canvas.Brush.Color := clBlack;
Canvas.FillRect(Rect(0,0,Width,Height));
end;
end;
end.
